Narratives, Chekhov’s Gun, and Agency
From a young age, I’ve always cherished trips to the movies with my mother. The allure of the big screen and the collective immersive experience have always captivated me. To this day, I find myself deeply absorbed in the narrative, often feeling as though I’m an invisible observer within the cinematic world. It’s as if I can sense the events unfolding around me.
After the credits roll, I often find myself pondering what makes the central character, or “hero”, truly heroic. Was the hero destined for greatness from the very start, or did this quality emerge as the story progressed? As someone who feels like a passive participant in the movie’s universe, I can’t help but question whether there was something inherently special about the hero that made their eventual role seem inevitable. In other words, did the hero recognize their destiny from the first scene, or was there a transformative journey involved?
Among the films I’ve watched, I’ve discovered a particular fondness for those that feature a significant character transformation over time. These narratives intrigue me because they suggest that the hero’s status is not predetermined. Instead, as an observer, I’m engaged in a dynamic process of trying to pinpoint who the hero might be at any given moment in the story. In a way, I’m constantly reevaluating and assigning the “hero” label as the plot unfolds.
As the movie progresses, my expectations continuously evolve. Reflecting on the film after the fact—knowing who the hero ultimately becomes—reveals that the most captivating movies are those where the transformation is most profound. At times, this hero is someone I never anticipated, which makes their journey all the more compelling and captivating.
Perhaps our fascination with movies and stories stems from two key elements: (i) they offer us a chance to explore realities that might be distant or unattainable in our own lives, and (ii) they are crafted by writers who control the narrative. Both aspects are crucial; the first provides a sense of transcendence, while the second grants us a sense of agency. It might not be a stretch to suggest that the stories we find most engaging and immersive are those that resonate deeply with our own desires and aspirations.
I find that movies centred around transformation particularly excite me. This naturally leads me to wonder what conditions set the stage for such transformations to unfold. To delve into this, I need to consider that the character faced a range of potential outcomes, some favourable and others less so. As the character moved through different stages of their journey, each choice they made influenced whether their path would ultimately lead them toward becoming the hero or away from it.
In essence, if we view the character’s journey as an unfolding movie, each step can be seen as a weighted function of various possible future events, determining their next move. Taking this argument to the limit, I view the weights assigned to potential outcomes evolving as a function of time. Reflecting on this, I realise that the assignment of weights to these possible outcomes is crucial. For the purpose of this article, I’d like to highlight two key aspects of this mental model:
-
Set of Potential Outcomes: I consider the set of potential outcomes to be fixed. What changes are the weights assigned to each outcome, which influence the subsequent steps. Thus, for simplicity, either the function that generates these weights converges towards a desired outcome or it does not. Thus, the true flexibility within this mental model resides in the choice of the weighting function, rather than in the predefined set of potential outcomes.
-
Control of the Weight Function: I assume that the choice of the weight function is under the character’s control. This assumption is quite significant because it implies the character has agency, which is a considerable leap.
One way to understand this is by reflecting on a principle from the movies I’ve always cherished. Great stories often embody the principle of narrative economy, where every detail and character serves a clear purpose, and nothing extraneous is included. This concept is captured by Anton Chekhov’s famous advice: “If you hang a pistol on the wall in the first act, it should be fired by the second act.” In other words, every element in a story must be relevant and impactful, contributing meaningfully to the unfolding narrative.
Applying this to our model, we view potential outcomes as various set of distributions representing reality, with one of these distributions being the optimal outcome. Each step over time is determined by a weighting function, which can either guide us (converge) toward the desired outcome or lead us astray (diverge).
In this framework, the character is Chekhov’s pistol—an indispensable element that must have a purpose. If the character were not meaningful, it would undermine the core narrative we’re exploring in my model. Thus, the character must have the agency to choose amongst different weighting functions.
To bring these abstract ideas into a more tangible context, I explored how to model them visually using mixtures of normal distributions.
In our model, we use mixtures of normal distributions to represent different possible outcomes or scenarios. Each normal distribution can be thought of as a bell-shaped curve, and each curve is associated with a specific mean (centre) and standard deviation (spread).
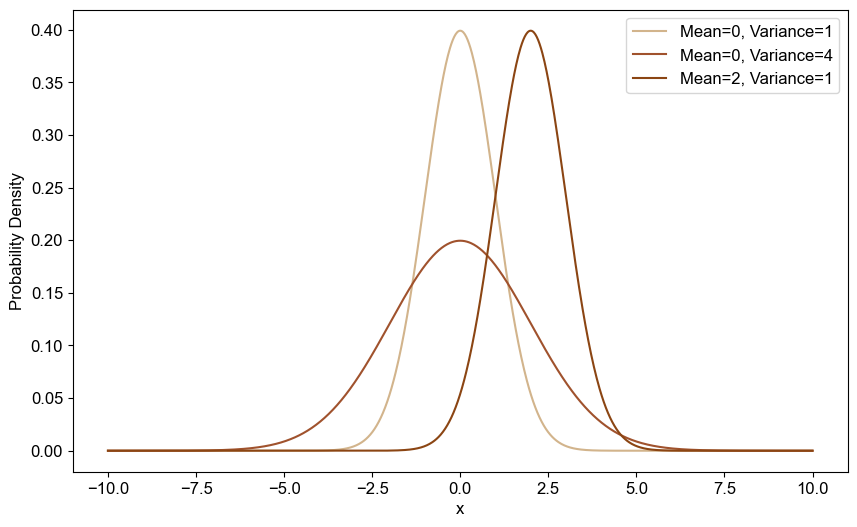
Imagine you have several such distributions, each representing a different possible outcome. For instance, one curve might represent outcomes where things are generally good, while another represents outcomes where things are less favourable. By combining these curves—known as mixing—you create a new curve that captures a broader range of possible outcomes.
The weighting function determines how much influence each of these normal distributions has at any given time. Think of the weighting function as a set of “rules” that tells us how to mix these bell-shaped curves together.
Here’s how it works:
-
Weights Over Time: The weighting function changes over time, and its shape dictates how the mix of normal distributions evolves. At one point in time, the weights might favour one distribution more heavily, while at another point, the weights might shift to favour a different distribution. This process can either lead to a convergence towards a single preferred outcome or show varying patterns over time.
-
Converging Weights: When the weighting function converges, it means that over time, the mixture starts to favour one particular normal distribution more and more. For instance, if we are converging towards a specific goal, the mixture will increasingly resemble the normal distribution that represents that goal.
-
Random Evolution: On the other hand, if the weights evolve randomly, the resulting mixture of distributions will continuously change in unpredictable ways. This can create a more dynamic and less predictable pattern in the combined curve.
Consider a scenario where you are mixing three normal distributions with different means and spreads:
-
Distribution 1: Mean = 0, Standard Deviation = 1
-
Distribution 2: Mean = 5, Standard Deviation = 1.5
-
Distribution 3: Mean = -3, Standard Deviation = 0.5
Let’s assume that Distribution 1 is our favourable distribution, i.e., distribution towards which we want our mixture to converge over time.
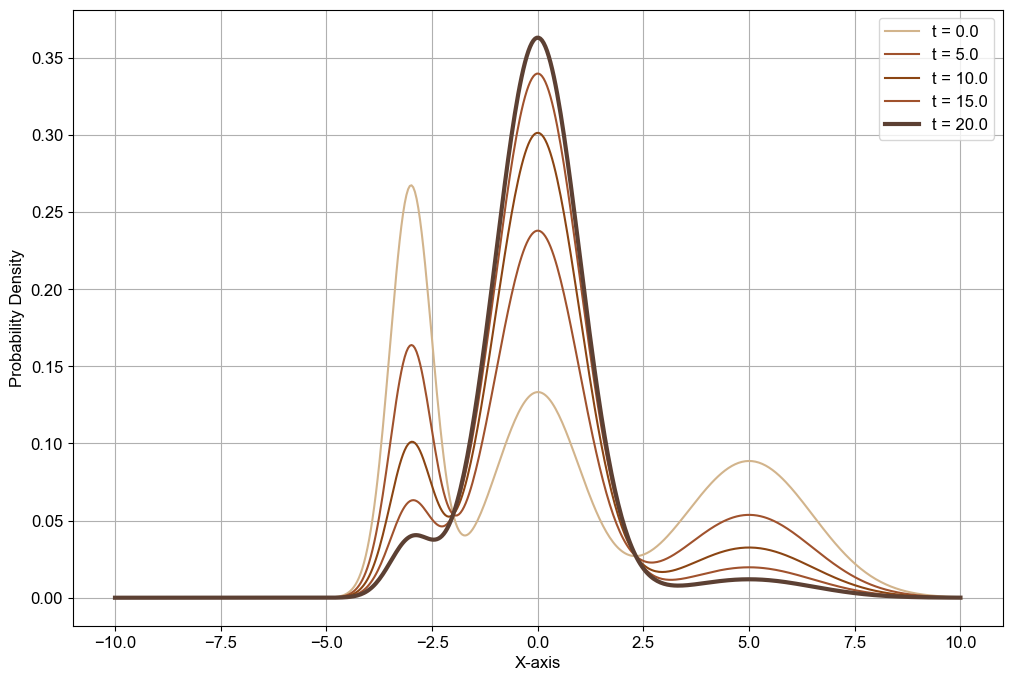
With Converging Weights (Image 2): At the beginning, all three distributions might be weighted equally. Over time, as the weighting function converges, the weights might increasingly favour Distribution 1 (mean = 0), making the resulting mixture curve more centred around 0.
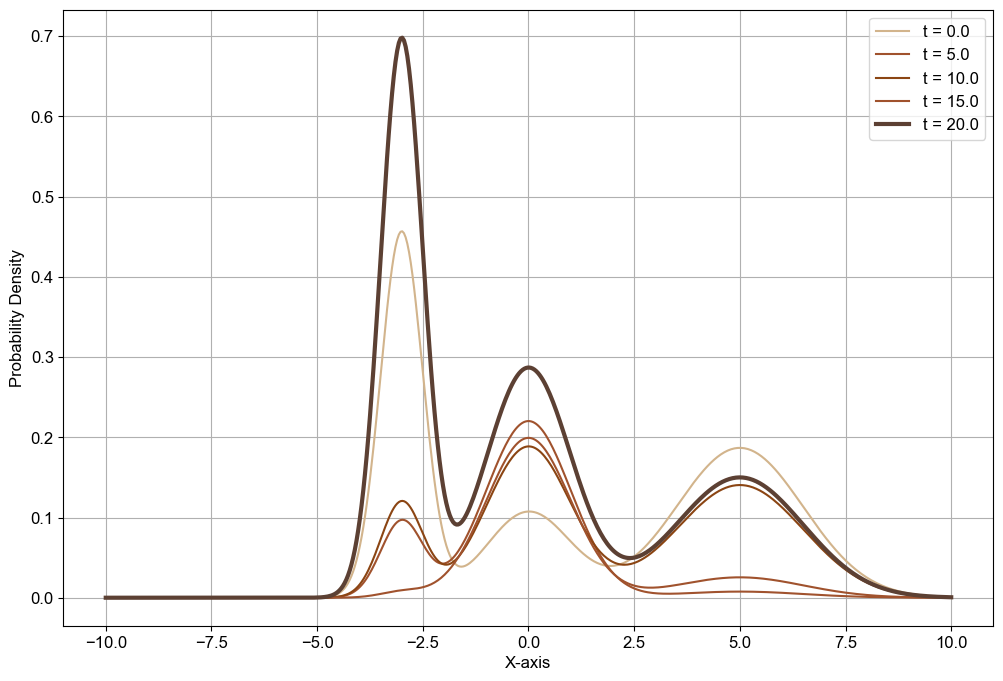
With Random Weights (Image 3): The weights might fluctuate randomly, leading to a mixture where the combined curve shifts and changes unpredictably, never settling into a single pattern.
When the weights converge over time, this is akin to our character gradually steering towards a desired outcome. This steady convergence represents a clear path and purposeful progression, where the final outcome aligns closely with the intended objective.
Conversely, when the weights evolve randomly, the result is a dynamic and unpredictable mixture that never settles into a stable pattern. This mirrors a scenario where our character faces constant change and uncertainty, akin to falling into the chaotic depths of unpredictability. The inability of the random weights to converge symbolises a struggle to reach a clear destination, reflecting the turbulence and disorder that our character might encounter.
Philosophically, I find several additional ideas (Image 4) about weighting functions particularly intriguing:
-
Acceleration and Deceleration: Introducing mechanisms that speed up or slow down the convergence process. This can help model how certain influences might rapidly shift the character’s trajectory or stabilise it over time.
-
Cyclicality: By incorporating cyclical patterns into the weighting functions, we can explore how periodic elements affect the character’s journey.
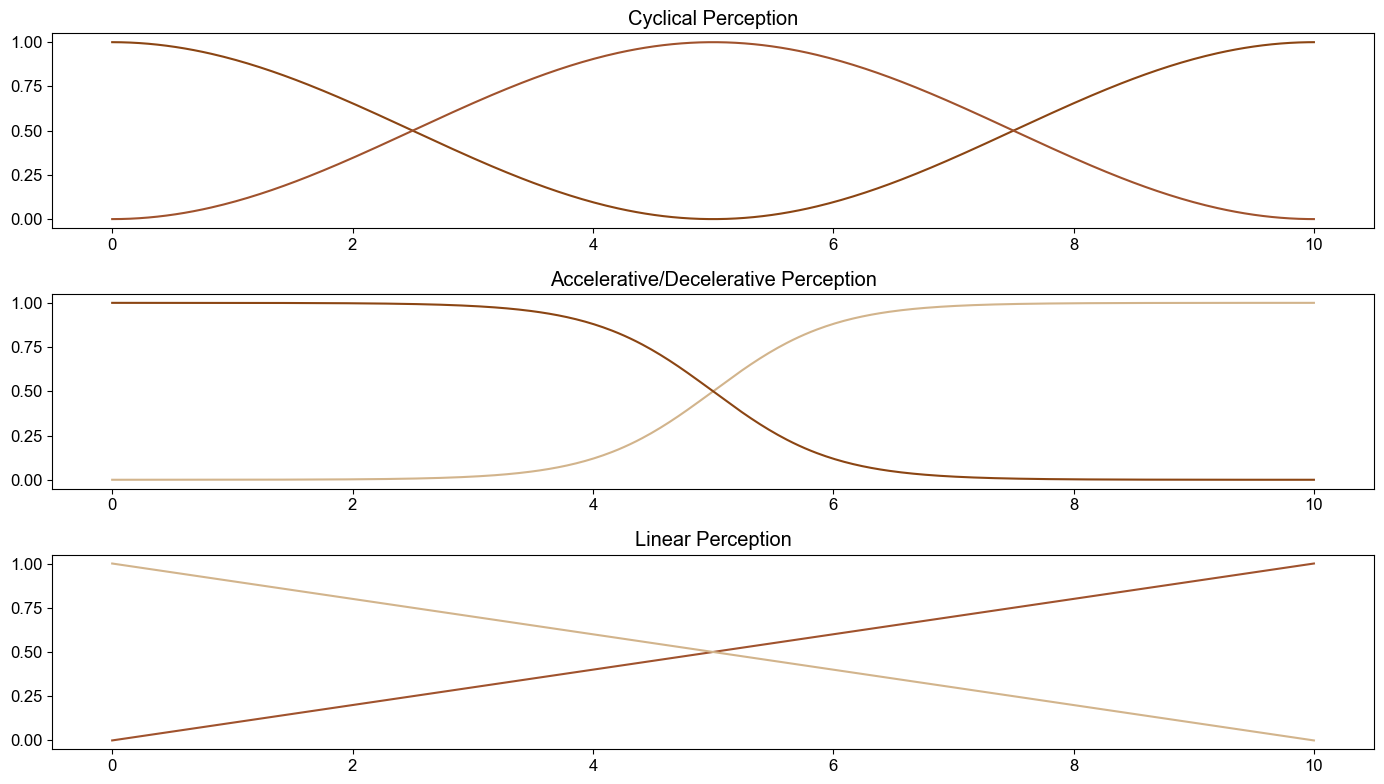
Ultimately, the choice of the weighting function—whether it converges towards a specific goal or evolves randomly—reflects the agency our character has in shaping their journey.
This decision is crucial, as it determines whether the narrative will progress towards a meaningful resolution or remain mired in chaos. The character’s ability to influence this choice highlights the central role they play.
Code on GitHub.